Option Greek Lesson: Managing the Vega, Gamma Tradeoff With an If-Then Matrix

We recently explored the ins and outs of two mostly ignored options Greeks. While most traders understand and even consider delta and theta, vega and gamma tend to be a bit too esoteric to bother studying. And, it's absolutely possible to be a successful options trader without ever thinking about these latter two Greeks.
For option trading fans that want to -- or need to -- use precision target prices or are specifically looking for certain gamma and vega profiles for use in what are often called "exotic" spreads, the challenge is significant. Gamma and vega, both of which are already only theoretical values, change in step with underlying changes in a stock's or index's price. They're also just additions to the thought process that can make things overwhelmingly complex.
There's a solution though. Traders can use calculators (online, spreadsheet add-ins, and outright software) to determine what a particular option's value would be at a certain point in the future at a certain price, with a certain degree of change in volatility. This way, a trader doesn't have to do any number crunching.
As is always the case, an example will help illustrate the important idea.
Let's hypothetically say we're looking to plug into a budding downtrend from Merck (MRK). We could buy a variety of put options with any number of strike prices and expirations. But, we want to try and pinpoint the where and when of the selloff so we can get the most bang for our (risk-adjusted) buck with the trade. In this particular case, we've got good reason to think the pullback could drag MRK down to a well-established support line just above $79.00.... let's call it $79.15. And, given the pace of the pullback thus far, it could take about a month to get there. We'll want to consider the calls expiring on February 28, which is 28 days from now.
We may know the when and where, but we don't know the which. That is to say, we've still got to choose the strike price that would bear the most fruit. To do that, we should at least think about delta and theta, and it wouldn't be a bad idea to consider gamma and vega.
Problem: That's a lot of number-crunching.
Solution: We'll let an option pricing spreadsheet that allows for multiple, comparative inputs to help us out.
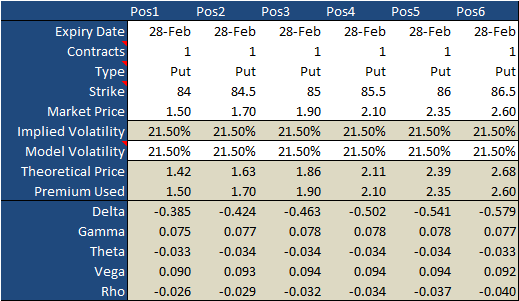
That's what the matrix below does for us. In this case we're using a proprietary Excel add-in, though similar tools exist for free on the internet if you look carefully. Notice how well the calculated theoretical values as of today (1/31/20) align with these options' actual prices.
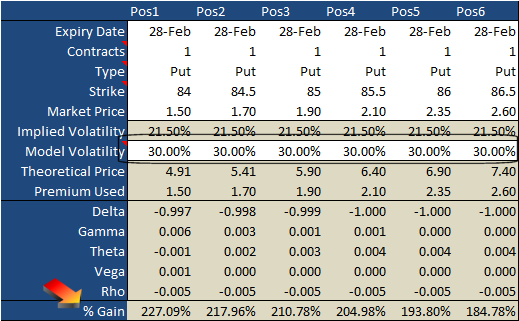
Now, look what happens when we change the date of calculation to February 26th (two days before expiration), and also change the price of Merck from its current price of 85.40 to our targeted price of $79.15.
As you would expect, the values of all the put options have grown tremendously. But, they've not grown uniformly. Some of the changes are surprising.
Yes, the cheapest option yielded the biggest gain. Namely, the 84 puts only cost $1.50 today, but they were worth (or would be worth) a theoretical value of $4.90 on February 26th, with Merck at $79.15. That's a 227% score. But, given the added risk of buying an out of the money put, the 85.50 puts that sold for $2.10 the day of the trade's entry produced a similarly healthy gain of 205%... without all the stress and worry. Even the 86.50 puts gained a respectable 185% for the timeframe.
What's most interesting is that the 84 puts had the lowest delta of all, which would have discouraged some traders. But, note that the 84 puts' gamma of 0.075 at the time of entry was almost as healthy as the 0.078 gamma the 85.5 puts were demonstrating at the time. In other words, the 84 puts' delta would change almost as much as the 85.5 puts' delta would change as the price of MRK changed. That's not something you'd see all that often... at least not to this degree of similarity. Usually, the gamma on out of the money options is markedly lower.
As for vega -- the measure of the impact of volatility on an option's price -- it was fairly uniform for all the options at the time of entry, only ranging from 0.09 to 0.094. Every penny counts, but these still would have just been pennies. As was the case with gamma though, one might expect a little less vega the further away you got from being at the money. (We see this a little bit, but not a lot.) This makes is a little easier to step into a cheaper option, though there's no major penalty for buying the more expensive 86.5 put.
But, this still isn't an entirely fair consideration of vega.
Should the price of Merck tumble from 85.30 to our target of 79.15, the volatility score isn't going to hold at 21.5%. It's apt to swell. We can't say how far, but a move like that just might push the implied volatility level up to 30%. In that scenario, the increase in volatility also does measurably more good for the cheaper, out of the money put options. That's not always necessary the case either. It was in this case, because vega was so uniform for all the options in question.
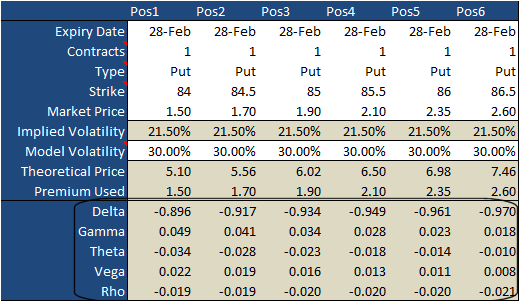
The point here, however, isn't to dissect the daylights out of vega and gamma. Indeed, in this particular case gamma and vega weren't particularly major factors leading to disparate outcomes. Sometimes they are. The point is, you can't feasibly tell with just a quick glance how things will take shape, but you also can't feasibly develop your own 'mental' matrix of six different if-then scenarios... each of which is made up of moving parts. To that end, and just for kicks, take a look at how different the Greeks looked a week and a half before expiration. They look dramatically different than they did at the trade's entry date, and they didn't change uniformly.
The moral of the story is, if you're going to worry about gamma and vega, do so in a way where you don't have to actually worry too much about figuring out all the scenarios by hand, or estimates. Automating all your what-ifs is the only way to effectively weigh one choice of option against another.
Of course, that all depends on picking a price target and timeframe first.
Also in this series:
- Option Greek Lesson: The Gamma Tradeoff
- Option Greek Lesson: The Vega Tradeoff
If you'd like to learn more about how to pick the right options, check out the BigTrends Boot Camps.