Option Greek Lesson: Vega Matters Even if You Don't Think It Matters

It's one of those things even many veteran option traders ignore, dismissing it as a distraction rather than helpful. And truth be told, if you never gave it a second thought, that would be ok. If you want to give yourself a surprising options-trading edge, however, vega can help. Here's why.

Vega is one of several so-called "greeks" often used by traders to give them a better feel for what an option is worth, and what that option might be worth at a different time in a different scenario. Most of the time traders start and stop their consideration of the greeks with delta and theta, the former of which tells you how much an option's value changes as the price of the underlying stock or index changes, while the latter just tells you how much value an option loses every day just due to the passage of time. Vega tells you how much an option's price is likely to change as the volatility of that stock or index changes.

As is usually the case, an example will help.

Let's use Microsoft (MSFT) calls as our guinea pig. Specifically, let's use the May 21st calls with a $250 strike in our illustration, which are in the money by $2.51 with Microsoft shares trading at $252.51, but are currently trading at a value of $6.90 per contract. That other $4.39 worth of premium is the speculative value, or time value, associated with taking such a bet on Microsoft at this time.

That $4.39 worth of extra premium isn't fixed though. Even if all other factors like time-until-expiration and the stock's closing price stay the same from one day to the next, the price of the 250 May-21 calls would still change if the intraday volatility (or intraday high-to-low ranges) change for the Microsoft shares.

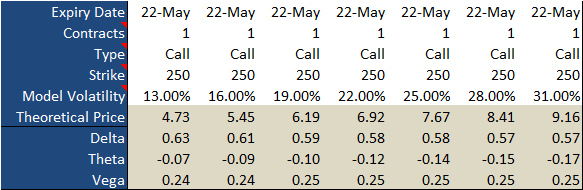
The grid below lays this idea out in a comparative format. At the stock's current volatility score of 22%, these calls are priced near the expected $6.90 per contract.... just a couple of cents below the modeled $6.92. Notice what happens if Microsoft stock's volatility is ratcheted up to 25% though. The call's price moves up to a theoretical $7.67 per contract. If volatility slides to 19%, the option would only be worth $6.19 per contract.

But, all of these changes could have been anticipated just by looking at vega, which is expressed on a per-contract basis for every 1% point increase or decrease in a stock's (or index's) volatility. In this case vega is 0.25, meaning for every 100 basis point (1%) change in Microsoft's volatility, the price of the calls themselves changes by $0.25. You can even check the math! If Microsoft's volatility slides to 19%, or three percentage points, the call's value falls from $6.92 per contract to $6.19. That's a difference of $0.73, versus an expected change of $0.75 (3% x $0.25). If instead we see Microsoft's volatility grow from 22% to 31%, or nine percentage points (900 basis points), the calls increase in value from $6.92 to $9.16. That's a difference of $2.24. The theoretical change would have been $2.25 (nine percentage points x $0.25).

The explanation of course raises questions, chief of which is how is the volatility of any stock or index calculated and disseminated? The full answer is too complicated to get into here, but the adequate answer is the Black-Scholes or other mathematical calculations. Most volatility scores look at the past 30 days' activity, and fall between 20% and 30% of the stock's price range during that time. Bigger changes in the daily closing prices bolster volatility, while smaller changes dial volatility back.

Make no mistake though. Volatility scores are an assumption. Nevertheless, vega values are surprisingly accurate indications of how an option's price will change... even if vega is an assumption too! "The market" does a pretty good job of pricing in what it knows, and then pricing in what it knows it can't know.

As for putting vega to use, it's an effective way to identify when an option may be overvalued or undervalued. It can indirectly help in setting price targets, even if that requires an assumption on your part on not how a stock's price might change, but how its volatility might change in the future.

Perhaps vega's best use, however, is helping you find and price credit spread trades (or even short option positions) when you want to sell puts and calls while volatility is pumping the price up but diminishing volatility will reduce an option's premium. In these trades you're essentially selling high and then buying low, but you want to sell as high as possible and then buy a low as possible. In these cases you can help yourself do that by being a net-seller when volatility is high, and then being a buyer -- or covering short trades, or unwinding credit spreads -- when volatility is low.

If you'd like to improve your overall options trading success, take a look at our online courses.