A Real-Life Example of the Option Greek 'Vega." (Spoiler Alert: It's Not What You Think.)
Vega. Not even veteran option traders are readily able to explain it, let alone utilize it in their trading. And, it's certainly not necessary to make good use of all that options have to offer. Still, knowing what vega is and how it works can't hurt.
To that end, here's a rundown of both, using a real-life example. It's a bit of a complicated walk-through, but if you pay close attention t will all make sense. You can decide after the fact if it's something you'll want to think about going forward.
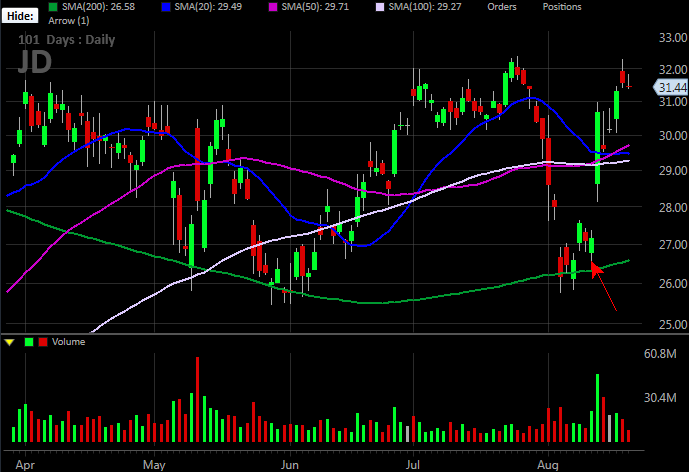
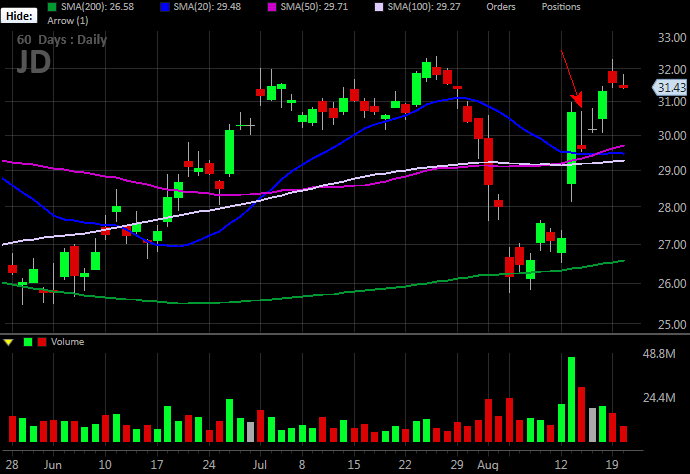
The guinea pig? JD.com (JD). It reported earnings on the morning of August 13th, but we want to start the 'journey' on the 12th, before the post-earnings volatility kicked in. The 12th is the bar marked with a red arrow on the daily chart of JD below.
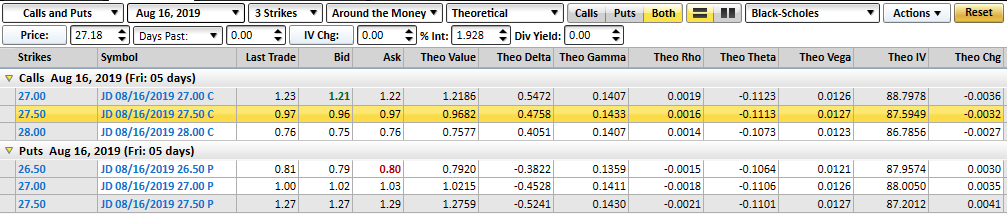
And, here's a look at all of JD's 'greeks' as of the 12th. We're going to focus in on the August 16th 27.50 calls, which at the time were closest to being at-the-money.
The delta here is, of course, 47.6 cents... about the typical for an option that's right at the money that's going to expire four days later. Theta, or time decay, stands at 11.1 cents per day. Again, that's about right. At the time, the option in question was priced at 97 cents (or $97 per contract). But, with a strike price of 27.50 when JD shares were trading at $27.18, the option itself had no actual intrinsic value at all. The entire 97 cents was all speculative value, or premium.
Most important, notice that vega then was 1.3 cents.
So, what is vega? In simplest terms it's a measure of the change in the price of the option for every 1% change in underlying volatility. To that end, notice that as of the 12th, JD's implied volatility is 87.6. Keep that number in mind.
As suspected, JD.com's earnings report created some volatility... a lot of it. Shares jumped 12.5%, or gained $3.41.
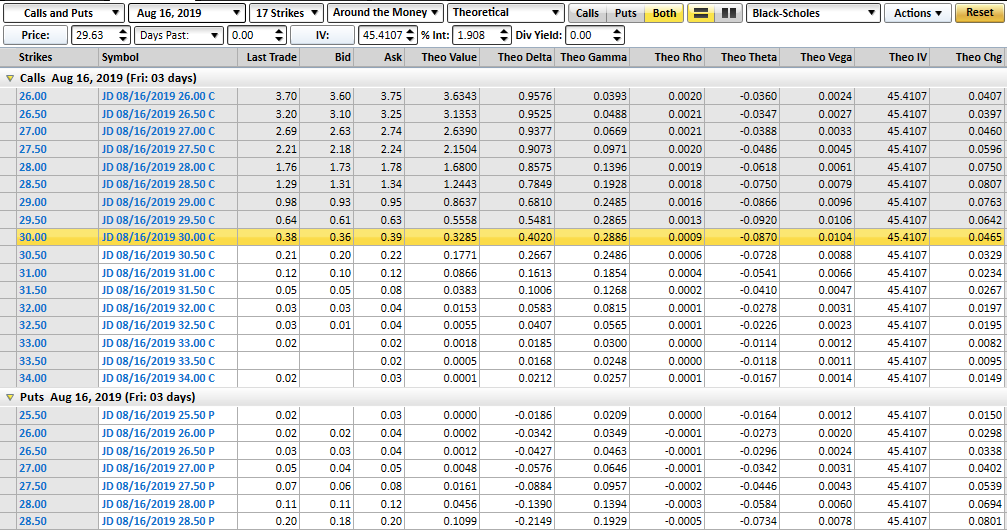
That move drove the price of the $27.50 calls to $3.51. Of that figure, $3.09 was true, intrinsic value. The other 42 cents was premium, or speculative value. Notice here that delta here was cranked up to 91.2 cents, and theta moved to 3.3 cents. Both were and are the norm. Notice the change in volatility and vega though. Volatility fell to 65.2, and vega fell to only 0.34.
This seems backwards. On a volatile day, volatility should be up, and presumably, vega would be up as well.
That's not how vega works though. Vega is a measure of what will probably happen in the future, based on the past. Volatility is a measure of what's likely to happen, based on the past. The implied volatility at the time recognizes that the pre-earnings jockeying was skewing option prices ... puts and calls. Once the proverbial cat was out of the bag and there was no speculating left to do, demand for (and interest in) those options faded.
More important, look at how when volatility subsided, the option's premium did too. As of the 12th, every bit of the option's price of 97 cents was premium, or speculative value. By the 13th, the option only saw 42 cents worth of premium. (A higher intrinsic value, yes, but not a higher premium, or time value.)
More to the point, for every 1% change in underlying volatility, there was supposed to be a 1.3% change in the option's price. Volatility changed - fell - by a factor of 22.4. That was supposed to mean about a 29.1 cent change in the price of an option, stripping out the impact of raw, intrinsic value's change. In the case of JD, the option in question saw 55 cents worth of net premium change between the two days.
All things considered, and given the circumstances, that's not bad. Those circumstances were of course a lot of speculative buying and selling in front of earnings. Even then though, we had a pretty good idea of how much the value of the August 16th 27.50 calls might change solely due to the impact of rising or falling volatility.
What's interesting is what happened the next day, the 14th, when the post-earnings surge further cooled off. Volatility fell to 45.4, but vega actually edge up from 0.34 to 0.45. (Remember, vega is not impacted by volatility, but rather, shows the impact of volatility.)
JD shares fell from 30.59 to 29.63 that day, obviously decreasing the value of the 27.50 calls. But, that decrease in value wasn't the same kind of decrease we saw the day before.
Now priced at 2.21 per contract, the 27.50 calls were intrinsically worth 2.13 apiece. The premium or time value fell to only 8 cents. Remember though, with a 19.8 point decline in volatility, we should have seen an inherent 8.9 point dip in the option's price at the time just due to weakening volatility. That's almost exactly what we got.
Confused? Don't be. Most people would have to read through the above example several times to fully understand. You should do the same, but with a specific mindset. That is, vega isn't impacted much by volatility, even though it's an indication of how volatility may impact an option's price. Go figure.
The inherent headache with worrying about vega is that in all cases it's an assumption rather than an calculation. While there's math behind the vega figure, it's usually rooted on a historical volatility and pricing history that isn't consistent. Sometimes, traders are just willing to pay more or less for an option. That can skew all the greeks in unexpected ways.
Perhaps more important, vega doesn't have a lot of value to traders except in very narrow instances where volatility is being traded more so than price changes. It can also be helpful when establishing price targets. It's proven most valuable to traders using multi-positioned trades and so-called 'exotics.'
For most option traders, vega doesn't mean a whole lot, and there's little you can do about it. If you're looking to capitalize on volatility though, a higher vega is certainly better than a lower one. As is the case with all-things-trading-related though, there's a tradeoff.