Option Trading School: What the Heck is Vega, and Do I Need to Care?
Even relatively new option traders know all too well that option pricing is quirky, and seemingly inconsistent. There are several variables -- some of which have been identified and quantified -- that explain the parts of the practice that don't make easy sense. They're called "the Greeks," and perhaps without even realizing it, novice option traders have been forced to think about the two chief ones... delta and theta. Delta is how responsive a particular option is to changes in the underlying stock or index's price, and theta is a measure of time decay, or a quantification of how fast an option loses value as its expiration approaches.
Delta and theta aren't the only Greeks option traders need to worry about though. There's also gamma, rho, and a real oddball called vega.
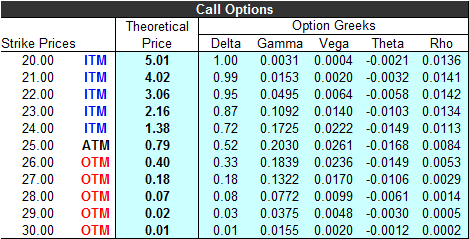
What's 'vega'? The working definition is a "measure of the impact of changes in the underlying volatility on the option price. Specifically, the vega of an option expresses the change in the price of the option for every 1% change in underlying volatility." It's usually expressed as a decimal, meaning a vega value of 0.08 would cause an option's value to change by eight cents for every 1% rise or fall in a stock's volatility. If a stock's volatility was 22% and but rises to 24%, those extra 2% points in volatility would cause that option's price to rise by 16 cents. Nothing else would have to change about any of the other factors that influence an option's value.
That's a significant increase or decrease in an option's value for just not-so-big changes in the underlying stock or index's volatility. The catch? It doesn't matter if rising volatility is bearish or bullish in nature. All increasing volatility increases the value of options... puts as well as calls.
It's a reality that points to the trickiness of option trading Indeed, it's vega that tends to cause so much headache for traders, even without those traders fully realizing it. Why's that? Two reasons.
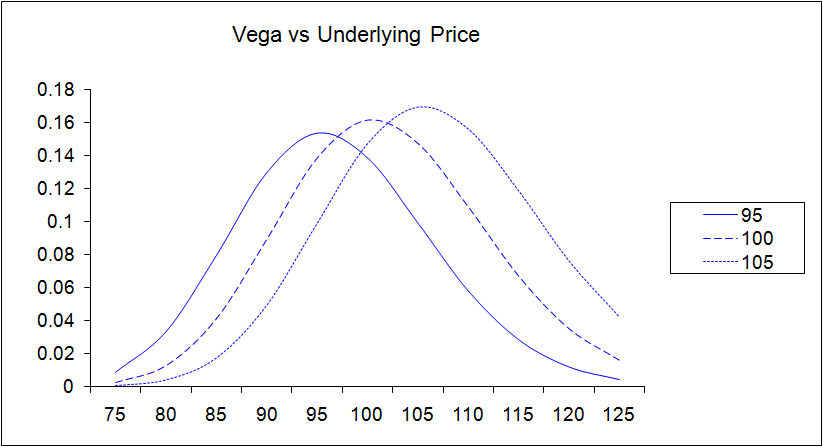
The first reason is, vega is inconsistent across the spectrum of stock prices. When a stock's price is at (or near) the money, vega is quite high. Just a few strikes away, vega is almost non-existent, making an option very insensitive to swings in the underlying volatility.
This makes sense. For option's that are well out of the money, even if a strong swell of volatility carries a stock much higher, the chances of that option moving to an 'in the money' status is still low. Conversely, even volatility surges and pushes a stock or index in the wrong direction, an in-the-money option is still going to be in the money. It's the options that are at or almost on the bubble of being in the money or out of the money that have the most to gain by increased volatility.
That variance can be a good thing, or a bad thing. But, it's a thing option traders have to understand. Just stick with options with a vega profile that makes more sense for your particular strategy? Not so fast. Every option has pros and cons. A high vega option -- if you want one -- generally costs a little more than an out-of-the-money option, and has a higher-than-average theta (or time decay). Lower-vega options that are out of the money are dirt cheap, but not all that responsive to price changes in the underlying stock or index. Lower-vega, deep in-the-money options sport a strong delta and a better theta, but they're expensive. The table below explains the relationship, though the table arguably understates how widely the greeks can vary.
The other headache is, while a direction or trajectory for a stock can be at least somewhat predicted, predicting volatility and changes in volatility is difficult, if not impossible. It's simply one of those things that's not knowable.
The $64,000 question: Does vega matter enough to think about it as you're trading, or is it all more or less built into the other greeks and an option's price?
If you didn't consider vega, even if you're a higher-level trader, it wouldn't be the end of the world. Many traders don't, and they do just fine. If you're taking on straddle trades though, because you're expecting an explosive move one direction or the other, vega can help you figure out just how far those options might rise or fall if-and-when that move transpires. It's conceivably possible that both sides of a straddle could increase in value, if volatility ramps up enough. A debit spread, conversely, would become even more profitable if volatility was unexpectedly reigned in.
Still, delta and theta mean so much more, and are so much more reliable in terms of trying to calculate their value and their impact.