A Practical Application of Vega in Credit Spreads

If you're like most new options traders, you probably don't worry too much about the predictive pricing measures called "the greeks." And, if you're like veteran options traders, odds are good you're mostly focused on delta and theta... which quantify (respectively) responsiveness to changes in the price of a stock or index and the amount of value an option loses each day solely due to the passage of time. Those two data nuggets can keep you too busy to worry about the lesser-watched greeks like gamma, vega, and rho.

Of those three though, the second one - vega - is worth keeping tabs on for a certain subset of options traders. Namely, spread traders (credit as well as debit) can squeeze out a few more profit points or save some money by paying a bit more attention to vega.

But, first things first. What the heck is vega?

The broad definition of vega is a measure of an option's sensitivity to implied volatility. More specifically, it's the presumed change in the option's price for a one-point change in a stock's implied volatility. It's also expressed as a decimal.

Here's an example: If an option is priced at 6.00 (or $600 per contract), its implied volatility level 15 and vega is .10, if the volatility cranks up to 25, then the option's value ratchets up to $7.00, or $700 per contract. The math is simple: 10 additional volatility points x 0.10 = $1.00. Assuming nothing else has changed, that $6.00 option contract is now worth $7.00. It works just the same for puts and calls.

Fine. But, in that you can't really predict increases or decreases in volatility, what good is knowing vega?

There's actually a lot of nuanced value in understanding what vega is and how it works, for a couple of reasons. One of them is, while you can't necessarily predict changes in how volatility may change, you actually can make reasonably educated guesses as to when extremely volatile stocks are apt to settle down, and when oddly tame stocks are due for some explosive action.

Where vega can really start to help, however, is when fans of option spreads are choosing trades.

Ever heard the term "selling volatility?" The underlying idea is simple enough. When you're selling volatility, it just means you're selling options at highly inflated prices due to upticks in volatility. Ideally, you're buying those options when volatility is in check, as that's when option premiums tend to be a bit lower than usual.

Credit spread traders looking to collect cash upfront for being a net seller of options (buying one contract, but selling another similar contract at a higher price) are often "selling volatility," perhaps without even knowing it. That is to say, they're hoping to sell high and then buy low to close out that spread trade. If vega is high at the selling point and low at the buying point - regardless of the sequence of those two transactions - that trader has squeezed out a bit more profit than he or she would have just from making the right directional call on a stock.

As is always the case, an example will help illustrate the idea.

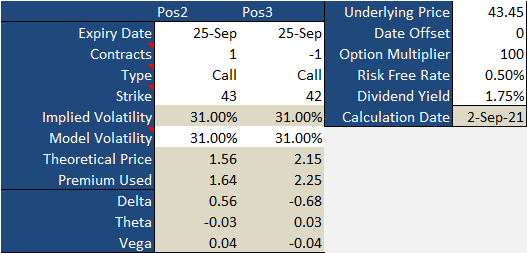
Let's assume Wells Fargo (WFC) is likely to continue falling from its current price of $43.45. To capitalize on this selloff and pocket some money upfront while its implied volatility is around 31%, we'll buy some 43 calls expiring three weeks from now at a price of $1.64, but we'll also sell some 42 calls also expiring three weeks from now at a price of $2.25 apiece. We keep the difference of $0.61, or $61 per contract. Here are the particulars (greeks and theoretical prices) of both legs of this spread upon our entry. Notice that the vega for both options is 0.04, meaning for every 1% rise or fall in Wells Fargo's volatility, both of these calls would automatically increase or decrease by $0.04. The 42 calls' vega is expressed as a negative figure since being short this contract, increases in volatility works against us. After all, we eventually have to buy this one back!

Now, check out what happens when we dial back the implied volatility from 31% to 25%. Specifically, check out the change to each call's theoretical price.

Did you catch it? The six percentage point decline in volatility whittled the value of the 43 calls down from $1.56 to $1.30, or $0.26. That makes sense. The vega of 0.04 multiplied by six percentage points equals $0.24, which is close to the $0.26 change in the option's theoretical value. Meanwhile, the 42 calls we shorted fell in value from $2.15 per contract to $1.92. That's a $0.23 change, which is very near the $0.26 change that vega predicted would be the case with volatility being dialed back from 31% to 25%.

Great, but astute traders and alert readers will immediately recognize that the price difference between the two calls now is still right around the same $0.61 we accepted as a credit when we entered the trade. If we closed out the trade, we'd be at no better than a breakeven.

And there's the problem... a problem that persists even if Wells Fargo shares lose value as expected and one week's worth of time passes. The positive vega on the long call and the negative vega on the short call are the same. We should have been looking for different vegas! Namely, we should look for spreads where the net vega (or the difference between the two vega figures) is net-negative. That is to say, the vega figure for the shorted option should be a bigger number than the vega figure for the long option. That way when volatility falls, the benefit of the short leg's value loss is greater than the downside of the loss of value for the long leg's price.

Again, an example will help.

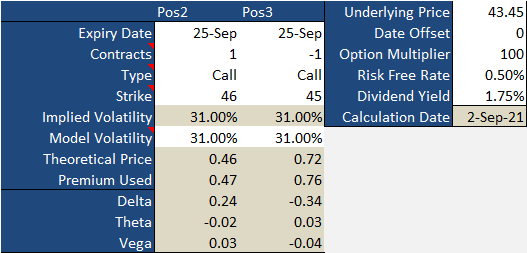
Sticking with the Wells Fargo example, let's swap out the 42 calls we shorted for some out-of-the-money 45 calls. And, let's replace the 43 calls we purchased with some 46 calls. Doing so changes everything about our price profile. Now this credit spread would put $0.26, or $26 per contract, in our pocket. That's the difference between the $0.72 we're selling the 45 calls for, and the $0.46 we're spending on the 46 calls. Here's that snapshot. Pay attention to the fact that we've got more negative vega with the shorted 45 calls than positive vega we've got with the 46 calls we own.

Now watch what happens when Wells Fargo's volatility shrinks from 31% to 25%. The option prices falls from $0.46 to $0.27 for the 46 calls, and from $0.72 to $.49 for the short 45 calls... a difference of $0.22. We could close out this trade right now with no other changes other than volatility at a small profit of $0.04, or $4.00 per contract. That's the difference between the net debit of $0.22 now and the net credit of $0.26 then.

It's not a thrilling profit to be sure, but keep the bigger picture in mind. A net-negative vega isn't the only thing that will work in your favor as volatility gets reigned in. It will, however, tack on a few more points to your overall gain. The nickels and dimes add up.

For the record, you don't always have to look at out-of-the-money options to capitalize on shrinking volatility, though that's usually going to be the case. You'll also find different vegas with differing expiration dates. You may also find that a net-negative vega for a prospective trade doesn't always make for a good trade, if the delta and theta figures aren't right. Keep in mind the same idea applies to bullish credit spreads using put options. The bigger point is, it pays to look at all the information you can when weighing a trade... including vega. You might find a meaningful, profitable detail you weren't expecting to find.