Most option traders understand the concepts of delta and theta. Delta, one of the so-called option "Greeks," is a measure of how responsive an option's price is to changes in the value of the underlying stock or index. Generally speaking, the higher the delta, the better. It means you're getting more bang for your buck. Theta, meanwhile, is a measure of time decay. In other words, theta indicates how much value an option loses every day just due to the sheer passage of time.
There are other options Greeks, however, esoteric though they may be. While not a necessity to understand and embrace, it sure wouldn't hurt a trader to at least understand these other measures of option-pricing dynamics. Perhaps one of the most important among the lesser-studied Greeks is vega [1].
Vega is simply the degree to which an option's price changes with respect to changes in the underlying assets volatility. The average stock's volatility — measured in percentage terms — is around $25. But, should that volatility ramp up to 30%, the price of an option will increase even if the price of that stock or index hasn't budged. For same traders that like to "buy volatility" (or "sell volatility [2]"), it's a number that matters.
The math is simple enough to understand. One only has to multiply the usually-theoretical vega figure by the difference in percentage points before and after. In the case above, were the vega for that instrument a fairly typical 0.14 for an option priced at $2.00, the increase in volatility of five percentage points would drive the price of that option up by a whopping 70 cents (0.14 x 5%). That would leave the option priced at $2.70, assuming nothing else has changed.
Don't get too excited yet. A increase in volatility of that magnitude is rather rare. A change of 1% is more akin to the norm.
To fully appreciate and understand the value of keeping an eye on vega, however, it's arguably best to demonstrate in terms of a comparison, or trade-off. Every option presents traders with a trade-off they must digest. The key is minimizing your particular pick's downside, and maximizing the upside.
The big tradeoff with vega — and let's assume you want the highest vega that's reasonably possible — is a large theta figure. That is to say, the higher the vega and the more explosive your option is likely to be, the faster the clock works against you.
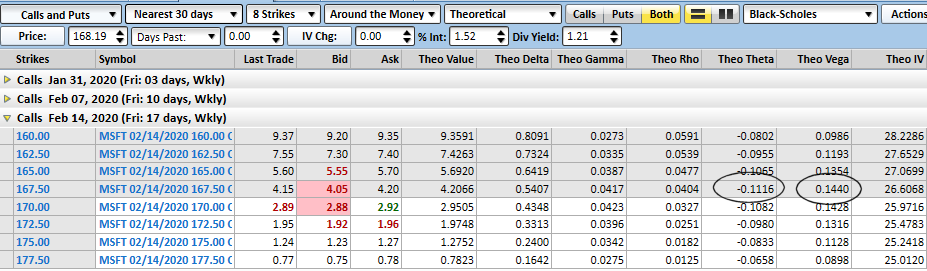
Take a look at the matrix of Microsoft calls below to see what this means. The options in question will expire a couple weeks out, and the ones being considered are all somewhere near the money. The highest vega choice is the 167.50 calls (also the one closest to being at the money), with a vega measure of 0.144. That means for every 1% increase in Microsoft's volatility, the 167.50 calls will increase their current value of $4.10 per contract by 14.4 cents. You'll also see, however, that for every day between now and mid-February, that contract worth $4.10 today will lose 11.1 cents worth of value… even if nothing else changes. That's also the highest theta value [3]of the call options on our matrix.
This actually makes quite a bit of sense. The time value makes up the lion's share of any premium value for an option above and beyond its intrinsic value. (The 167.50 call in question is mathematically only worth 57 cents, when the price of MSFT is at $168.07. The other $3.53 is the premium other traders are willing to pay just to bet Microsoft shares will be much higher a couple of weeks from now.) As such, this at-the-money call is decidedly on the fence right now. It's the one that will lose or gain the most value from here, but traders are quickly losing interest in holding this least certain bet. However, a small increase in volatility would also most dramatically assure option traders that the 167.50 calls are going to rapidly gain value.
How do we know this? Because the 167.50 calls also sport the highest gamma on the board despite a very moderate delta measure. But, that's another story. The big take-away for here and now is, if you're going to try and capitalize on upticks in volatility, know that you're going to be racing the clock more so than you might with other options of around the same strike and expiry.
As for what sort of balance you might expect to find between the two, notice in our example above that the vega was a little bit greater than theta… though not leaps and bounds so. That ratio is more or less the norm, although it's hardly the absolute.
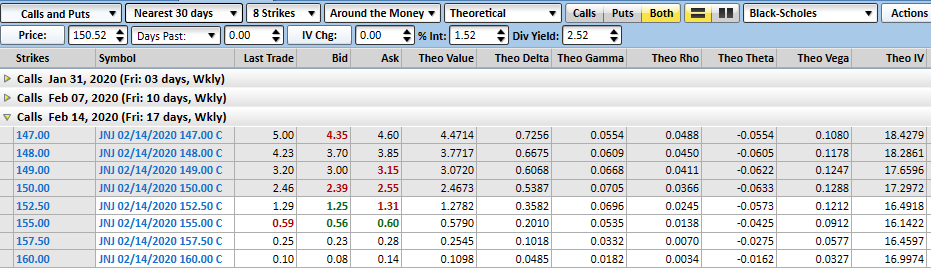
Take for instance Johnson & Johnson's nearby call options. The at-the-money calls with a strike price of $150 expiring a couple of weeks from now sports a vega of 0.128, but a theta of only 0.063. This is a name that would benefit nicely from increasing volatility, but wouldn't over-penalize you just for holding it a few days.
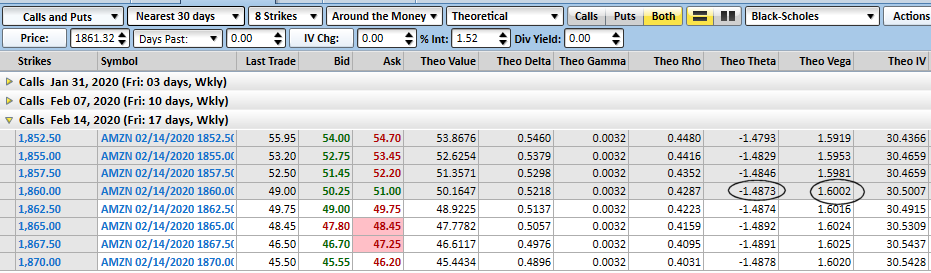
At the other end of the spectrum, Amazon's 1860 calls expiring in two weeks show a vega of 1.60, but a theta of 1.48. This is a particularly uncoupling prospect for trying to make money on increased volatility, as AMZN shares are likely always "maxed out" on volatility. Its volatility is currently scored at 30%, and isn't actually likely to get much higher.
That's not to suggest Amazon can't be the basis of a good option trade. But, if you're counting on volatility to increase to pump up the value of the option — and some spread traders do just that — this isn't a top prospect. You're really fighting time decay in a big way.
Again though, the lesson to be learned here is that high responsiveness to volatility doesn't come free. The price is paid in other ways, as it always is, but it's particularly paid on the time front. That's the big vega tradeoff.
If you'd like to get better at trading options and learn all the ins and outs of all the Greeks, try one (or all) of the BigTrends Trading Bootcamps [7].